Gamma Family of Distributions

What’s there?

This one explores some more distributions – Gamma, Chi-Squared, and Student’s t-distributions. Why?

The Gamma distribution provides a flexible model for positive continuous random variables, such as waiting times.
The Chi-Squared and Student’s t-distributions are special cases and transformations derived from the Gamma and Normal distributions.

Why do I write this?

I wanted to create an authoritative document I could refer to for later. Thought that I might as well make it public (build in public, serve society and that sort of stuff).

Gamma

It is a continuous distribution defined on the positive real line. This just means that it’s defined for $x > 0$ .

Foundations

We’ve described the gamma function in Uniform, Exponential, Beta & Dirichlet. As a recap, it is,

$\Gamma(z) = \int_0^\infty t^{z-1}e^{-t} dt$

Back to the topic, what are we even trying to do? What’s the intuitive goal?

We want to model the waiting time until the $\alpha$ -th event occurs in a Poisson process with a rate of $\beta$ .

Recall the Exponential distribution models the waiting time for the first event. The Gamma distribution generalizes this to the sum of waiting times for multiple events.

Before everything, I just want to recap Poisson from Fundamental Discrete Probability Distributions.

The Poisson distribution is a statistical tool used to model the probability of a certain number of events happening within a fixed interval of time or space, provided these events occur at a known constant average rate and independently of the time since the last event.

For instance, “How many emails will I receive in the next hour?”

$P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!}$

Where:

k is the number of events you are interested in (e.g., 5 phone calls).

λ (lambda) is the average number of events per interval (e.g., an average of 3 phone calls per hour).

e is Euler’s number (approximately 2.71828).

k! is the factorial of k.

Theory

Formal Definition: A continuous random variable $X$ follows a Gamma distribution, denoted $X \sim \text{Gamma}(\alpha, \beta)$ , if its PDF is:

$f(x | \alpha, \beta) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha-1}e^{-\beta x}, \quad x > 0$

The distribution is governed by two parameters:

Shape parameter ( $\alpha > 0$ ): Controls the shape of the distribution. For $\alpha \le 1$ , the density is monotonically decreasing. For $\alpha > 1$ , it has a single peak. As $\alpha \to \infty$ , the Gamma distribution approaches a Normal distribution.
Rate parameter ( $\beta > 0$ ): Controls the scale of the distribution (inverse of the scale parameter).

Moments:
- Expectation: $\mathbb{E}[X] = \alpha/\beta$
- Variance: $\text{Var}(X) = \alpha/\beta^2$
Relationship to other distributions:
- If $\alpha=1$ , the Gamma distribution becomes the Exponential distribution: $\text{Gamma}(1, \beta) = \text{Exp}(\beta)$ .
- The sum of $k$ independent $\text{Exp}(\beta)$ variables is a $\text{Gamma}(k, \beta)$ variable.
- The Chi-Squared distribution is a special case of the Gamma distribution.

Why is this cool?

The sum of independent Gamma-distributed random variables with the same rate parameter is also a Gamma-distributed variable. Specifically, if $X_i \sim \text{Gamma}(\alpha_i, \beta)$ are independent, then:

$\sum_{i=1}^k X_i \sim \text{Gamma}\left(\sum_{i=1}^k \alpha_i, \beta\right)$

The shape parameters add, while the rate parameter remains the same.

Chi-Squared (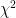 $\chi^2$ )

First principles

The Core Definition: Let $Z_1, Z_2, \dots, Z_k$ be $k$ independent random variables, each following a standard normal distribution, $Z_i \sim \mathcal{N}(0, 1)$ . The Chi-Squared distribution with $k$ degrees of freedom, denoted $\chi^2_k$ , is the distribution of the sum of the squares of these variables:

$Q = \sum_{i=1}^k Z_i^2 \sim \chi^2_k$

Degrees of Freedom ( $k$ ): The single parameter of the distribution, $k$ , is the degrees of freedom. It corresponds to the number of independent standard normal variables being summed. It dictates the shape of the distribution.

Fundamental theorems of calculus

First one

If $F$ is an antiderivative of a continuous function $f$ on an interval $[a, b]$ , then:

$\int_a^b f(x) \,dx = F(b) - F(a)$

Second one

If $f$ is a continuous function on an interval, then for any $a$ in that interval, the function defined by $F(x) = \int_a^x f(t) \,dt$ is an antiderivative of $f$ . That is:

$\frac{d}{dx} \int_a^x f(t) \,dt = f(x)$

Ok, cool, what if $a$ was function of $x$ ? This is the Leibniz Integral Rule.

If you have an integral of the form:

$F(x) = \int_{a(x)}^{b(x)} f(t) \,dt$

Its derivative with respect to $x$ is:

$\frac{dF}{dx} = f(b(x)) \cdot b'(x) - f(a(x)) \cdot a'(x)$

As a special case of Gamma

Step 1: Find the distribution of $Y = Z^2$ where $Z \sim \mathcal{N}(0, 1)$ .

We can derive this using the change of variables technique. Let $F_Y(y)$ be the CDF of $Y$ . For $y > 0$ :

$\begin{aligned} F_Y(y) &= P(Y \le y) \\ &= P(Z^2 \le y) \\ &= P(-\sqrt{y} \le Z \le \sqrt{y}) \end{aligned}$

This probability is the integral of the standard normal PDF, $\phi(z) = \frac{1}{\sqrt{2\pi}}e^{-z^2/2}$ , between $-\sqrt{y}$ and $\sqrt{y}$ :

$F_Y(y) = \int_{-\sqrt{y}}^{\sqrt{y}} \frac{1}{\sqrt{2\pi}}e^{-z^2/2} dz$

We find the pdf using the Leibniz Integral rule –

$\begin{aligned} f_Y(y) = \frac{d}{dy} F_Y(y) &= \phi(\sqrt{y}) \cdot \frac{d}{dy}(\sqrt{y}) - \phi(-\sqrt{y}) \cdot \frac{d}{dy}(-\sqrt{y}) \\ &= \frac{1}{\sqrt{2\pi}}e^{-y/2} \cdot \frac{1}{2\sqrt{y}} - \frac{1}{\sqrt{2\pi}}e^{-y/2} \cdot \left(-\frac{1}{2\sqrt{y}}\right) \\ &= 2 \cdot \frac{1}{\sqrt{2\pi}}e^{-y/2} \cdot \frac{1}{2\sqrt{y}} \\ &= \frac{1}{\sqrt{2\pi}} y^{-1/2} e^{-y/2} \end{aligned}$

Now, we compare this PDF to the Gamma PDF, $f_X(x; \alpha, \beta) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha-1}e^{-\beta x}$ .
We need to match the terms.

The exponential term $e^{-y/2}$ suggests the rate parameter is $\beta = 1/2$ .
The polynomial term $y^{-1/2}$ suggests that the shape parameter is $\alpha-1 = -1/2 \implies \alpha = 1/2$ .
Let’s check if the normalization constant matches. For $\text{Gamma}(1/2, 1/2)$ , the constant is $\frac{(1/2)^{1/2}}{\Gamma(1/2)}$ . It is a known property of the Gamma function that $\Gamma(1/2) = \sqrt{\pi}$ . So the constant is $\frac{1/\sqrt{2}}{\sqrt{\pi}} = \frac{1}{\sqrt{2\pi}}$ .
This matches perfectly. Therefore, we have proven that the square of a single standard normal variable follows a Gamma distribution:

$Z^2 \sim \text{Gamma}\left(\alpha=\frac{1}{2}, \beta=\frac{1}{2}\right)$

A Chi-Squared distribution with one degree of freedom is identical to this Gamma distribution: $\chi^2_1 = \text{Gamma}(1/2, 1/2)$ .

Step 2: Find the distribution of $Q = \sum_{i=1}^k Z_i^2$ .

Since each $Z_i^2$ is an independent $\text{Gamma}(1/2, 1/2)$ random variable, we can use the additive property of the Gamma distribution. The sum of $k$ such variables will be:

$Q = \sum_{i=1}^k Z_i^2 \sim \text{Gamma}\left(\sum_{i=1}^k \frac{1}{2}, \frac{1}{2}\right) = \text{Gamma}\left(\frac{k}{2}, \frac{1}{2}\right)$

By definition, $Q \sim \chi^2_k$ . Thus, we have established the equivalence:

$\chi^2_k = \text{Gamma}\left(\alpha = \frac{k}{2}, \beta = \frac{1}{2}\right)$

Where is this distribution used?

Example 1: Testing the Variance of a Population (Goodness-of-Fit)

Scenario: A manufacturer produces bolts that are supposed to have a diameter variance of $\sigma^2 = 0.01 \text{ mm}^2$ . To perform quality control, a sample of $n=20$ bolts is taken, and their sample variance is calculated to be $s^2 = 0.015 \text{ mm}^2$ . Does this provide significant evidence that the true variance of the manufacturing process has increased?
Application: Under the null hypothesis that the population is normal and the true variance is indeed $\sigma^2=0.01$ , the test statistic:

$\chi^2_{\text{stat}} = \frac{(n-1)s^2}{\sigma^2} = \frac{(19)(0.015)}{0.01} = 28.5$

follows a Chi-Squared distribution with $n-1=19$ degrees of freedom. We can then compare this value to the $\chi^2_{19}$ distribution. We would calculate the probability $P(\chi^2_{19} \ge 28.5)$ . If this probability (the p-value) is very low (e.g., < 0.05), we would reject the null hypothesis and conclude that the manufacturing process variance has likely increased.

Example 2: Likelihood-Ratio Tests in Machine Learning

Scenario: In machine learning, we often want to compare two nested models: a simpler model (e.g., linear regression) and a more complex model that includes the simpler one as a special case (e.g., polynomial regression). We want to know if the additional complexity of the second model provides a statistically significant improvement in fit.
Application: Let $L_0$ be the maximum likelihood value for the simple model and $L_1$ be the maximum likelihood for the complex model. The likelihood-ratio test statistic is:

$D = -2 \log \left( \frac{L_0}{L_1} \right) = 2(\log L_1 - \log L_0)$

According to Wilks’s theorem, as the number of data points becomes large, this statistic $D$ approximately follows a Chi-Squared distribution. The degrees of freedom $k$ are equal to the difference in the number of free parameters between the two models. This provides a formal statistical test for model selection and is used to justify adding parameters to a model.

We will discuss this later as well under statistics.

Student’s t-

Why does this exist?

Z-statistic

The formula $Z = \frac{\bar{X}-\mu}{\sigma/\sqrt{n}}$ is a way to standardize the sample mean. It tells us how many standard errors our sample mean ( $\bar{X}$ ) is away from the true population mean ( $\mu$ ). If we know the true population standard deviation ( $\sigma$ ), this Z-score will perfectly follow a standard normal distribution (a bell curve with a mean of 0 and a standard deviation of 1). T

This is wonderful because the properties of the normal distribution are well-understood, making it easy to calculate probabilities and test hypotheses.

But, we know neither $\sigma$ nor $\mu$ .

This is where the Student’s t-distribution comes in. It was developed specifically to solve this problem.

Since we don’t know the population standard deviation ( $\sigma$ ), we have to estimate it using the sample standard deviation ( $s$ ). We then substitute $s$ into the formula, creating a new quantity called the t-statistic:

$t = \frac{\bar{X}-\mu}{s/\sqrt{n}}$

To account for this added uncertainty, the t-statistic doesn’t follow a perfect normal distribution. Instead, it follows a t-distribution.

Theoretical development

Formal Definition: Let $Z \sim \mathcal{N}(0, 1)$ be a standard normal random variable and $V \sim \chi^2_k$ be a Chi-Squared random variable with $k$ degrees of freedom. If $Z$ and $V$ are independent, then the random variable $T$ defined as:

$T = \frac{Z}{\sqrt{V/k}}$

follows a Student’s t-distribution with $k$ degrees of freedom, denoted $T \sim t_k$ .

Derivation of the t-statistic: In the context of the sample mean, we have $Z = \frac{\bar{X}-\mu}{\sigma/\sqrt{n}}$ and we know that $V = \frac{(n-1)s^2}{\sigma^2} \sim \chi^2_{n-1}$ . Substituting these into the definition of $T$ :

$T = \frac{\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}}{\sqrt{\frac{(n-1)s^2/\sigma^2}{n-1}}} = \frac{\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}}{\sqrt{s^2/\sigma^2}} = \frac{\bar{X}-\mu}{s/\sqrt{n}}$

This statistic, which uses the sample standard deviation $s$ , follows a t-distribution with $n-1$ degrees of freedom.

Importantly,

The t-distribution approaches the standard normal distribution as the degrees of freedom $k \to \infty$ . This makes sense: as the sample size grows, our estimate $s$ of the true standard deviation $\sigma$ becomes very accurate, and the uncertainty from estimating it vanishes.

Where is it used?

Machine Learning (t-SNE): As discussed previously, the t-distribution with one degree of freedom is used in the low-dimensional space of t-SNE to create embeddings where clusters are more clearly separated. Its heavy tails are the key to this property.

Hint for Hypothesis Testing: The t-distribution is the basis for the Student’s t-test, one of the most widely used statistical tests. It is used to compare the means of two groups, or to test whether a sample mean is significantly different from a hypothesized value, when the population variance is unknown. The t-statistic $\frac{\bar{X}-\mu}{s/\sqrt{n}}$ is calculated, and its value is compared to the critical values of the t-distribution to determine statistical significance. It is the go-to tool for inference on means with small sample sizes.